1 FST3 Library Architecture
For simplified global overview of FST3 library architecture see Fig. 1. Key entities involved in FS process have their counterparts in respective FST3 classes Search, Subset, Criterion, Classifier and Model. All data access is abstracted through a specialization of class Data_Accessor (see Fig. 2 for details). Concrete search algorithms (specializations of Search, see Fig. 5 for details) yield a Subset object, maximizing a chosen criterion (specialization of Criterion, see Fig. 4 for details). Note that gray boxes in Figs. 2, 4 and 5 suggest points of straightforward library extension. For examples of library usage click here.
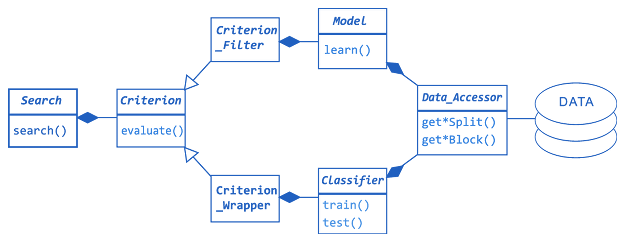
Figure 1: FST3 library architecture - simplified global overview. The call to search() returns a feature subset with respective criterion value
2 FST3 Data Access Layer
Access to data is realized through a Data_Accessor object. Data_Accessor provides standardized access to data for all library tools that need so, including Criterion and Classifier objects. The default data accessor specializations, Data_Accessor_Mem_ARFF and Data_Accessor_Mem_TRN, respectively, cache in memory complete data read from a file in ARFF or TRN format (see Figs. 2). Accessing different data sources (e.g., a database server) requires deriving a new class from Data_Accessor.
Two data access modifying mechanisms are implemented through dedicated objects: data pre-processing and multi-level data splitting to training/testing data parts (see Fig. 2).
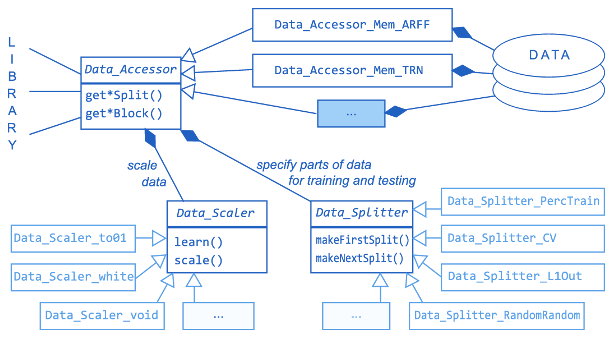
Figure 2: FST3 library architecture - simplified view of data access classes
Data_Scaler objects enable data preprocessing, primarily aimed at normalization of data values. Concrete Data_Scaler is called during Data_Accessor initialization. Default normalizers include Data_Scaler_to01 to scale all values to [0,1], Data_Scaler_white to normalize mean values and variances, and Data_Scaler_void to by-pass the mechanism.
Data_Splitter objects enable sophisticated access to various parts of data at various stages of the FS process. The mechanism enables to realize various estimation schemes, selecting data parts for training/validation/testing, as well as FS stability evaluation.
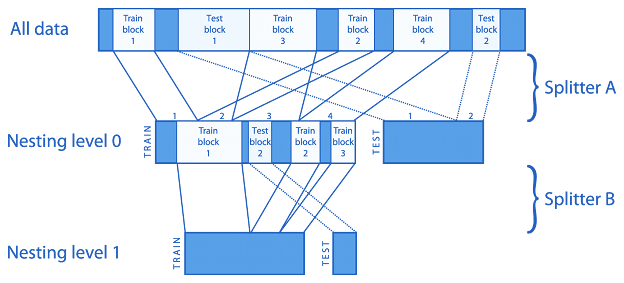
Figure 3: FST3 data access layer - nested train/test splitting
Splitters may provide multiple loops of data access (in k-fold cross-validation there would be k loops). The splitting mechanism allows nesting to arbitrary depth (see Fig. 3). Typically two nesting levels suffice; the "outer" spliting level is good for separating test data for final verification of FS results, the "inner" splitting level is good for estimating classifier accuracy in each step of wrapper-based FS selection process. Different Data_Splitter objects can be used in different nesting levels. Just one nesting level is set for data access at a time to hide the nesting mechanism from higher-level library tools (where simple access to training and testing data is expected). Each Data_Splitter object generates two lists of Data_Intervals (intervals indexing data samples), one to select data samples for training, second to select data samples for testing. Technically there is no restriction on possible interval overlapping (i.e., data sample re-use), nor on completeness of data coverage. See Fig. 3 for illustration. Default FST3 splitter objects implement cross-validation (class Data_Splitter_CV), hold-out (class Data_Splitter_Holdout), leave-one-out (class Data_Splitter_Leave1Out), re-substitution (class Data_Splitter_Resub), random sampling (class Data_Splitter_RandomRandom).
Remark: splitting can be defined separately for each class or globally. Separate splitting leads to stratified data sampling (proportional with respect to class sizes). Global splitting enables, e.g., leave-one-out access where in one loop only one sample in one class is accessed for testing while all others in all other classes are accessed for training.
3 FST3 Feature Subset Evaluation Framework
See Figure 4 for overview of FST3 subset evaluation class hierarchy. Abstract class Criterion_Filter covers the implementations of independent criteria, class Criterion_Wrapper adapts Classifier objects to serve as dependent criteria. Several independent criteria and classifiers require first to estimate Model parameters from data.
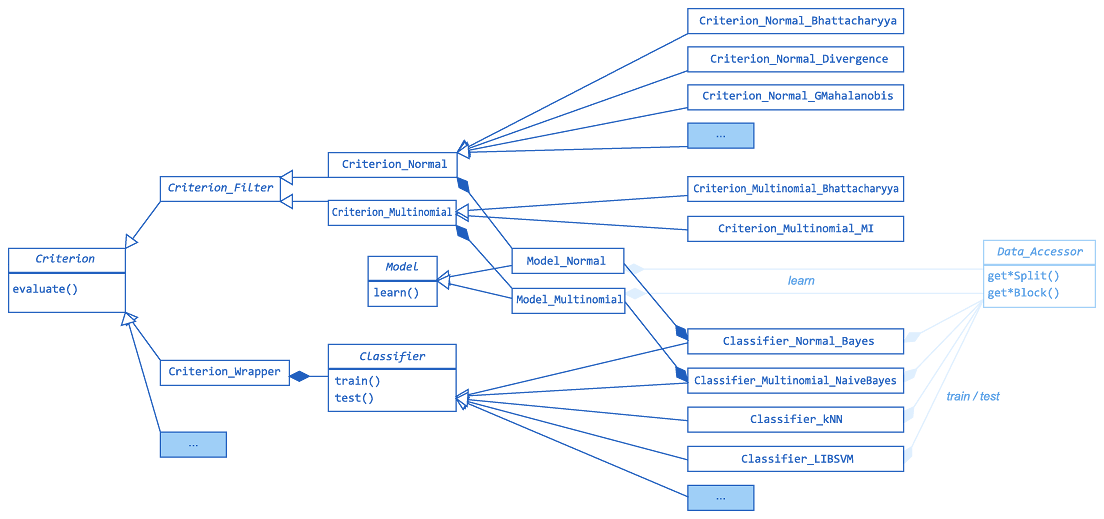
Figure 4: FST3 library architecture - implemented subset evaluation criteria, data modeling and classifier classes
3.1 Data Models
Class Model_Normal implements the multivariate gaussian (normal) model. Note that criteria based on normal model may yield misleading results for non-normally distributed data, especially in multi-modal case. Class Model_Multinomial implements the multinomial model, suitable esp. for text categorization. Model_Normal is used in Criterion_Normal-based criteria and Classifier_Normal_Bayes. Model_Multinomial is used in Criterion_Multinomial-based criteria and Criterion_Multinomial_Naive_Bayes.
3.2 Classifiers and Dependent Criteria
Class Classifier_Normal_Bayes implements Bayes classifier assuming normally distributed data, class Classifier_kNN implements k-Nearest Neighbor classifier, class Classifier_LIBSVM provides interface to externally linked Support Vector Machine library, class Classifier_Multinomial_Naive_Bayes implements Naïve-like Bayes classifier assuming multinomially distributed data. Class Criterion_Wrapper adapts any object of type Classifier to serve as FS criterion, see Fig. 4.
3.3 Independent Criteria
Class Criterion_Normal_Bhattacharyya implements Bhattacharyya distance, Criterion_Normal_GMahalanobis implements generalized Mahalanobis distance, Criterion_Normal_Divergence implements the Divergence, all assuming normality of data. Criterion_Multinomial_Bhattacharyya implements multinomial Bhattacharyy distance, Criterion_Multinomial_MI implements individual Mutual Information.
4 FST3 Feature Subset Search Framework
FST3 implements a battery of search algorithms that cover the broad variety of search complexity scenarios. See Figure 5 for overview of FST3 search algorithms' class hierarchy.
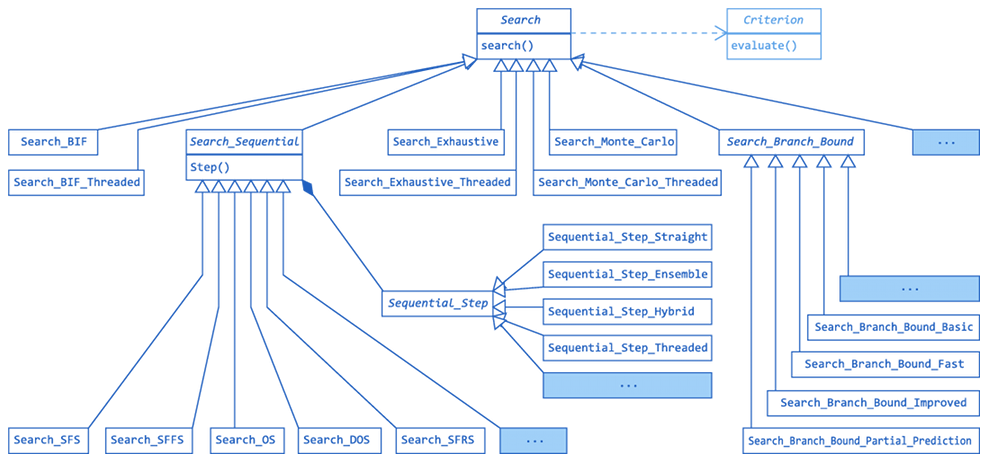
Figure 5: FST3 library architecture - implemented search algorithm classes
4.1 Ranking
The simplest and fastest method is feature ranking (BIF, best individual features), implemented in class Search_BIF. By evaluating each feature separately BIF runs in linear time at the cost of ignoring possible inter-feature dependencies. In terms of achieved criterion value for the final subset BIF is easily over-performed by any of the following methods, yet it is the most robust and possibly most reliable option in small sample scenarios.
4.2 Sequential Search Methods
The more powerful sub-optimal sequential search methods generally follow the hill-climbing idea. To avoid local extremes the more advanced methods extend the hill-climbing idea by introducing various forms of backtracking and/or randomization. Sequential search methods do not guarantee optimality with respect to chosen FS criterion, yet they offer very good optimization-performance vs. (polynomial) time-complexity ratio, making them the favourable choice in FST3. The battery of implemented methods includes d-parametrized sequential search, floating search, oscillating search, and d-optimizing retreating search and dynamic oscillating search.
4.3 Exchangeable Sequential Search Steps
All FST3 sequential search algorithms take use of one Sequential_Step derived object. The standard Sequential_Step_Straight object implements the operation of adding/removing one feature to/from the current working subset so that the new subset yields maximum criterion value possible. Using alternative step objects instead enables various alternative search schemes. Sequential_Step_Hybrid turns any sequential search algorithm into a hybridized procedure. Sequential_Step_Ensemble enables multiple feature selection criteria to be used as voting ensemble in order to reduce over-fitting and improve stability.4.4 Parallelised Search
FST3 enables parallel evaluation of feature selection criteria. This ability can be directly utilized in all search methods derived from Search_Sequential through the use of Sequential_Step_Straight_Threaded object instead of the standard Sequential_Step_Straight. Parallelism in feature selection context scales well as candidate feature subsets can be evaluated independently of each other in search algorithm steps. Parallelism significantly extends the limits of which problems can be considered tractable in terms of maximum problem dimensionality and/or sample size.4.5 Result Tracking
FST3 enables tracking of all/part-of intermediate solutions that the search algorithms evaluate in the course of search. Objects derived from Result_Tracker make it possible to eventually identify alternative solutions to the single one provided by standard search methods. Result_Tracker_Dupless can reveal alternative feature subsets yielding the same criterion value. Result_Tracker_Regularizer makes it possible to select alternative solutions based on any secondary criterion. Result_Tracker_Stability_Evaluator enables feature selection process stability evaluation.4.6 Optimal Methods
The only optimal method applicable with arbitrary Criterion is the exhaustive search, implemented in Search_Exhaustive and Search_Exhaustive_Threaded. Optimal Branch & Bound-type methods are significantly faster than exhaustive search, yet they are restricted for use with monotonous criteria - in FST3 context to Criterion_Filter descendants. Note that all B & B algorithms are principally exponential, therefore can not cope with problems of dimensionality exceeding roughly 40-50.
5 FST3 Specialized Tools
FST3 provides specific tools for specific purposes.
5.1 Very-High-Dimensional Feature Selection
In problems of dimensionality exceeding thousands or tens of thousands it is assumed that due to the extreme number of possible subset combinations it is hardly possible to select features using any other method than individual ranking (Search_BIF and Search_BIF_Threaded in FST3). However, oscillating search (in its fastest setting) has been shown applicable in very-high-dimensional context to improve solutions obtained in other way (e.g., by means of ranking). FST3.1 adds a novel alternative method - dependency-aware feature ranking (DAF) - which evaluates features on a (large) group of subset probes using an arbitrarily chosen Criterion (wrappers are permitted!), to eventually rank features individually according to their averaged behavior in context. DAF is capable of producing results significantly better than BIF in very-high-dimensional settings at the cost of longer but still reasonable compuational time (in the order of hours or dozens of hours for 10000-dimensional experiment). See demo34 and demo35t for more details.
5.2 Stability, Similarity, Feature Acquisition Cost, Missing Values
FST3 provides tools to evaluate the stability of feature selection process, to evaluate similarity of two feature selection processess or to estimate wrapper bias. Low stability usually indicates over-fitting, and thus poor expectable performance on independent data. FST3 also provides a selection of tools for less common scenarios, like feature selection with respect to known feature acquisition cost, or in situations with incomplete data.
See References for formal descriptions of implemented tools.

